Interactive Minkowski diagram / spacetime diagram

The diagram in a pop-up window - Tutorial - Examples and excercises - Answers - Sources

This interactive Minkowski diagram is based on the conventional setting of c = 1. Units along the axis may be interpreted as: t unit = second, then d unit = lightsecond, or alternatively, d unit = m, t unit = 3.34E-9 s, etc. As usual, the three spacial dimensions are represented by the single d axis. Alternatively, you may use c as a conversion factor and read the vertical axis in length units as ct in stead of c. Then both axes may be read in meters.

The diagram is representing a model of two spacetime events, event A and event B. Two observers in two inertial reference frames pass each other in the origin. At that point is event A - the green ball. The user inputs the time and distance for event B - the red ball - and the relative velocity. The diagram will show time dilation, the relativity of simultaneity and other effects of special relativity.

The diagram will show the events as measured by the two observers as designed by Einstein: Each observer has a set of synchronized clocks and previously established distance points. The diagram may also show the observed times as calculated by taking into account the travel time of light from the events to the observers.

One observer follows the worldline of t, the other follows a worldline t' which will appear when the button "Calculate" is pressed. First input the relative velocity as a fraction of c, time and distance for event B as measured by the observer following worldline t.

Calculation of coordinates in the t' system are done by the inverse Lorentz transformations. The input values are as measured in the t coordinate system that is not moving. With c = 1 the simplified inverse Lorentz transformation is lorentz_id and lorentz_it .

For some situations where the goal is to find the coordinates in the t system, the simplified original Lorentz transformation is used. A reminder of those equations:

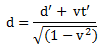lorentzd and lorentzt .

The initial setting is to use the inverse Lorentz transformations. The choice of input and mode of calculation may be toggled with the button " Toggle input mode ".

The two events may also be shown in "real time" by pressing the buttons " Play worldline t " or " Play worldline t' ". The two events will then appear in space and time (given time unit = 1 second).

Below the animation is a more detailed tutorial and some examples and excercises.

Relative velocity: c	Event A:	d = 0	t = 0
	Event B:	d =	t =
		d'=	t'=
		Invariant interval:
		i² = (ct)² - d² = i'² = (ct')² - d'² =

Time = s

Tutorial

The animation may be opened in a separate window by clicking this link.

Basic input

The user can input 3 variables, relative velocity and the distance value and time value for event B. Values are entered in the fields as shown above.

The relative velocity is entered as a fraction of c, the speed of light (299 792 458 m/s). Velocities >= 1 or <= -1 are not accepted.

Event A is always at t = t' = 0 and d = d' = 0.

When the button Calculate is pressed the animation will calculate the time and distance values for event B as measured by the observer in the worldline t'. These values are shown in the grey output fields.

The animation will also calculate the invariant spacetime interval (the Lorentz interval) squared.

The animation calculates and displays the slope and scale of the worldline t' depending on the relative velocity. The distance line d' associated with the worldline t' is also displayed.

The button Toggle input mode toggles the calculation mode of the animation and the respective input variables. In the initial setup the animation is using d and t as input and calculates with the inverse Lorentz transformations. Using the toggle button you may instead use d' and t' as input and calculate with the original Lorentz transformations.

The button Clear resets the display area, the user input and the calculated variables.

The graph

Event A is shown with a green ball. Event B is shown with a red ball.

To find the distance of event B in the t reference frame, follow the grey line from the red ball and parallel to the t (ct) axis and read off the d axis.

To find the time of event B, follow the grey line from the red ball and parallel to the d axis and read off the t (ct) axis.

When the t' (ct') axis and the d' axis are shown, the spacetime coordinates for event B are found in a similar way.

To find the distance of event B in the t' reference frame, follow the blue line parallel to the t' (ct') axis and read off the d' axis.

To find the time of event B in the t' reference frame, follow the blue line parallel to the d' axis and read off the t' (ct') axis.

Notice that the t' (ct) and d' axes are scaled according to the inverse Lorentz transformation in order to show the correct time and distance values.

Real-time playback

The two Play buttons will activate playback on the distance-lines. The time will progress as shown by the clock, and the two events will appear as predicted by the respective measurements according to the two worldlines. This display is most effective with sound activated as the two events are accompanied by a couple of chords. Event A appears at d = 0 and t = 0 and at d' = 0 and t' = 0.

Observation times

The Minkowski diagram shows the events as measured according to the reference frames. This should not be confused with observations of the events. Unless event B lies directly on the worldline of one of the observers, observation time will be different from measured time. To show the observation times it is necessary to calculate the travelling time for the light from the event to the observers. The animation can show the light path and the observation times.

When the Show/Hide button is toggled on, the graph shows the light path from event B to the two observers at t' and t as a yellow line. Since light moves at v = c = ±1 in this diagram, these lines are always at ±45^o to the t and d axes. The observation times are marked on the two worldlines and shown in a connected text field. To the right is an example.

The observation info may be removed from the graphic by toggling the Show/hide button.

Examples and exercises

1) Slope and stretch of worldline for the moving observer.

Input t = d = 0, ie., both events are at the origin at time 0. Input relative velocity 0.3 c. Notice the slope of worldline t' and the approximate distance between the time and distance markers. Change the velocity to 0.5 c and recalculate. Notice that the angle between the t and the t' axes has increased and that the distance between the markers has increased.

Excercise 1a: Try other velocities like 0.7 c and 0.8 c.

Excercise 1b: Now study the d' axis when different velocities are chosen. What is the relationship between the angle between t and t' and the angle between d and d'?

2) Change point of view

If observer t' moves at velocity v in relation to observer t, one may change the point of view and say that observer t moves at velocity -v in relation to observer t'. The two velocities are equal in magnitude and opposite in direction. If we change the point of view of the motion, the locations of events A and B will be exchanged as well. What was d and t for event B is now d and t for event A and vice versa.

An example: Input v = 0.6 c, d = 5, t = 6. Notice that d' = 1.75 and t' = 3.75. Now switch point of view by inputting v = -0.6 c, d = 1.75 and t = 3.75. Notice that now d' = 5, t' = 6. In other words, the change in point of view keeps the same coordinates for the two events.

Excersise 2a: Input v = 0.25 c, d = 6, t = 4. Switch point of view. What are the new input values?

Excercise 2b: Input v = 0.8 c, d = -1, t = 2.5. Switch point of view. What are the new input values?

Excercise 2c: Input v = -0.6 c, d = -5.5, t = 5. Switch point of view. What are the new input values?

3) Time dilation and the slowing of clocks.

Toggle the input mode so that the d' and t' fields are active. Input v = 0.6 c, d' = 0 and t' = 4. This indicates that both events are on the worldline of the moving observer. Suppose both events represents a tick of a clock that ticks every second. From the moving observer's point of view, the clock shows that 4 seconds has passed. Notice that the nonmoving observer measures that 5 seconds has passed. The nonmoving observer will conclude that the moving clock is slow.

Now turn the situation around. Toggle the input mode so that the d and t fields are active. Input v = 0.6 c, d = 0 and t = -4 (negative 4). The clock is now on the worldline of the observer that is at rest. Since the distance is the same, 0, for the observer we are following in the respective situations, it must here have taken the moving observer some time to reach this point in the reference frame of the observer at rest. So the time is input as negative this time. The nonmoving clock shows that 4 seconds has passed. But according to the moving observer, 5 seconds has passed. The moving observer will correctly conclude that the nonmoving clock is slow.

Conclusion: Both observers will conclude that the other clock is slow (by a factor of 4/5 = 0.8).

Note that in the first situation, the observer t measures that the distance in fact is 3, and the moving observer measures the distance as 0. In the second situation, the observer t measures the distance as 0, and the moving observer the distance as 3.

Excercise 3a: Repeat this experiment with v = 0.8 c. What are the d and t values for the nonmoving observer be when the moving observer's clock shows t' = 1.5? What is the rate of time dilation each observer will calculate for the other clock?

Excercise 3b: Repeat the experiment with v = 0.5 c. What are the d and t values for the nonmoving observer when the moving clock shows t' = 3? What is the rate of time dilation?

Excercise 3c: After observing the slowing of clocks for 3 different velocities, 0.5 c, 0.6 c and 0.8 c, what will you conclude regarding the relationship between the relative velocity and the time dilation?

4) Simultaneity

Let v = 0 and input d = 4, t = 0. The two events A and B are simultaneous in both reference frames. Now change the velocity to v = 0.4 c. Notice that t' changes to -1.7457. This means that in the reference frame of the moving observer event B is measured to happen almost 2 seconds before event A, they are not simultaneous. But in the nonmoving reference frame they are still happening at the same time!

Change the relative velocity to v = -0.4. Now event B is measured to happen almost 2 seconds after event A according to the moving observer. To conclude: Events that are simultaneous to one observer are generally not simultaneous to another observer moving relative to the first one.

Repeat this experiment as above, with the two different v-values. Each time, click the buttons Play worldline t and Play worldline t' respectively and follow the animation of the events as measured by the two observers. Notice when and where the two events appear in both cases.

Another example. Input v = 0.6 c, d = 3.75 and t = 2.25. Notice that t' = 0. Event B is now simultaneous to event A in the reference frame of the moving observer, but not in the nonmoving reference frame. Here event B happens 2.25 seconds after event A. Notice that event B is placed on the axis d'. All points on this axis are simultaneous to the origin in the moving reference frame. Likewise: All points on any line that is parallell to d' are equidistant in time from the origin in this reference frame.

Use the "Play worldline"-buttons also for this experiment and for the two exercises that follow!

Excercise 4a: Two observers are moving at 0.8 c relative to each other. For one observer two events A and B are simultaneous and separated by 3 units of space. How will the two events be measured by the other observer?

Excercise 4b: At a relative velocity of 0.8 c, what will the nonmoving observer measure if the moving observer measures event B to be simultaneous with event A and at the distance of 1.5? (Hint: Use the input mode for the original Lorentz transformations.)

5) Temporal order

Under some conditions the temporal order of events may be any of these: Before, simultaneous or after. An example: Let event B be located at d = 4, t = 2. First, try v = 0.2 c. Both observers now agree that event A happens before event B. Change the velocity to v = 0.5 c. Now the two events are simultaneous according to the moving observer. Finally set v = 0.8 c. This time the moving observer will measure event B to happen before event A. All three possibilities of temporal order are present, only depending on the velocity of the observer. Use the Play worldline-buttons for all three scenarios to confirm the numerical and graphical data.

Excercise 5: Set v = 0.6, d = 5 and t = 1. Then find a velocity where the two events are simultaneous for the moving observer and a velocity where event A happens before event B for the moving observer.

Examples 4 & 5 demonstrate clearly that there is no such thing as absolute simultaneity.

6) The invariant interval

In special relativity there is a quantity that is invariant (not changing) for all inertial reference frames. In other words, given some event B one can calculate an interval which is the same regardless of the relative velocity of the two observers. The equation for this interval (also called the Lorentz interval or the invariant spacetime interval) is given by i² = (ct)² - d². The animation calculates the square of the invariant interval .

Example: Set v = 0.3 c, d = 3, t = 4. Notice that i² = i'² = 7. Try changing the velocity, e.g set v = 0.5 c. Try any other value for v. Try a negative value for v.

Excercise 6: Find the invariant interval for d = 5.5, t = 2.5. Find the invariant interval for d = 2, t = 6.

[In three spacial dimensions the Lorentz interval is given by the equation i² = (ct)² - (x² + y²+ z²).
(In some texts the sign is switched between the time and space dimensions).]

7) Timelike and spacelike intervals

In the animation the spacetime diagram is divided by the two lightlines into 4 equal sectors. Two of these are labelled "Timelike intervals", two "Spacelike intervals". Choose any value for v and plug in these value-pairs for d and t: d = 5 t = 3, d = 6 t = -1, d = -5 t = 4, d = -6 t = -3. Notice that all instances of event B are in the sectors with spacelike intervals. Notice also that for all these instances the spacetime interval squared is negative. In all such cases the spacial relation between events A and B cannot be reversed. With spacelike intervals the spacial separation dominates, d² > (ct)², and there can be no causual relationship between the two events. Another way to view this: The interval is such that there is not enough time for light to pass from one event to the other.

Now choose any value for c and plug in these value-pairs for d and t: d = 1 t = 2, d = 3 t = 5, d = -1 t = 6, d = 4 t = -5, d = -3 t = -6. Notice that all instances of event B are in the sectors with timelike intervals. Notice also that for all these instances the spacetime interval squared is positive. In all such cases the sequence in time between events A and B cannot be reversed. With timelike intervals the separation in time dominates, (ct)² > d², and there is no fixed directional relationship between the two events: left and right can be exchanged depending on the motion of the ovserver.

There is a third type of interval to consider. Let (ct)² = d² which is to say v = d/t = c. In other words, the velocity is c, the speed of light. This type of interval is therefore called lightlike and it is represented in the animation by the two yellow worldlines representing light passing through event A.

Excercise 7: Given that event A as usual is in the origin, decide which of the intervals are spacelike, timelike and lightlike for the following events B. Use both the numerical and the graphical method to decide. Also use the "Play worldline"-function and various velocities to confirm your choice.
a - d = 3, t = 5. b - d = -3, t = -6. c - d = 5, t = 1.5. d - d = -3.5, t = 3. e - d = 2.0, t = 2.1. f - d = 4.5, t = 4.5.

8) Observations

The two observers will see event A simultaneously, at t = d = 0. When will they see (observe) event B? To find out, one must calculate the travel time for light from event B to the worldline of the two observers. The button: Show/hide light path to observers activates the calculation and shows the light paths to the observers. Input v = 0.4 c, d = 4 and t = 4.5. Calculate and toggle the Show/hide button. Notice that the nonmoving observer measures event B to happen at t = 4.5 but he sees the event at t = 8.5. The moving observer measures event B to happen at t' = 3.1642 and she sees the event at t' = 5.5646. Notice the angle of the light path. Notice that the same light path passes through both observers.

Excercise 8a: What is the angle of the light path relative to the time axis t?

9 The twin paradox

The twin paradox is the well-known fact that someone travelling at a relativistic speed ages more slowly than someone at rest. This can be demonstrated by an experiment with a pair of twins where one twin travels an interstellar distance and back at high speed.

Let event A₁be the separation of the twins and event A₂ the reunion. These events are both on the t worldline of the twin that stays at home (ie, at rest). Event B is the turn around point for the travelling twin. This event must therefore be on the t' worldline. To achieve this we must set the values such that d / t = relative velocity. Let us try v = 0.75, d = 3 and t = 4. Note that t' = 2.6458, this is the elapsed time for the traveller. Elapsed time for the stay-at-home twin is of course 4. Now the travelling twin turns around. The return trip therefore has v = -0.75 and d = 3 and t = -4. t must be negative to achieve the negative relative velocity. An alternate reasoning is that the event A₂ which is the common event when the two twins are back together again has the values t = d = 0, and to achieve this t and t' for event B on the return trip must be negative. Note that t' = -2.6458 and t = -4. Time elapsed must be the negative of this result since we started the home lap with a negative time value. Total elapsed time for the travelling twin is thus 2.6458 * 2 = 5.2916. And total elapsed time for the stay-at-home twin is 4 * 2 = 8.

Conclusion: the travelling twin ages slower! This is of course not really a paradox: The stay-at-home twin is staying in the same inertial reference frame but the travelling twin is switching reference frame at the turn around point. This can also be seen from the fact that the worldline of the stay-at-home-twin is continuous (vertical both times) but the travelling twin has two different worldlines with - in this case - an angle of about 74^o.

Excercise 9a: Use the animation to calculate how much younger the travelling twin is after travelling 24 light years and back at 0.96 c. (Hint: Start by finding the travel time at 0.96 c!)

Excercise 9b: Use the animation to calculate how far you can travel and return while 500 years pass at home and you travel at 0.9999 c. What is your elapsed time as a traveller?

10) Length contraction

To use the Minkowski diagram to calculate and show the Lorentz-Fitzgerald length contraction requires some special consideration. Suppose we have an object of a certain length, say 7 units. What would it entail for the two observers to measure the length of this object? The nonmoving observer has no problem, the object is not moving relative to him, so he can use his distance axis d. We know that all points on this axis are simultaneous in the nonmoving reference frame. The moving observer also needs to measure the length of the object by measurements simultaneous at both ends of the object. That is only possible along the d' axis or a line parallell to this axis. We know that all points on the d' axis are simultaneous for the moving observer. In the case of the d' axis we also know that the time t' at all points is 0.

Input v = 0.3 c and d = 7. The meaning of this is that the rest length of the object is 7 units, and this is the length the nonmoving observer measures. How can we find t? This equation from the inverse Lorentz transformation will help: lorentz_it

We know v and d, and we also know that t' = 0 since we are only interested in points along the d'-axis. This fact simplifies the equation to t - vd = 0 and t = vd. With v = 0.3 and d = 7 we easily calculate that t = 2.1. Intput this result.

Notice that this gives d' = 6.6776. This demonstrates that the object is shorter by appr 0.3224 when the velocity is 0.3 c.

Now input some new values: v = 0.4 c, t = 0.4 * 7 = 2.8. The result is now d' = 6.4156.

Excercise 10a: Find the length contraction at v = 0.5, 0.6, 0.7, 0.8, 0.9, 0.95, 0.99, 0.999 and 0.9999 c.

Notice that the length contraction increases more rapidly with increasing velocity. Notice also that the length contraction becomes extreme when v approaches c.

Excercise 10b: Suppose the object is moving along with observer t'. Find out how to use the animation to calculate the length contraction when v = 0.3 c and d' = 7. (Hint: Use the original Lorentz transformation, not the inverse!)

Answers to excercises

1b: The two angles are equal in size and opposite in direction.

2a: v = -0.25 c, d = 5.164, t = 2.582.

2b: v = -0.8, d = -5, t = 5.5.

3a: Event B happens at d = 2 and t = 2.5 in the rest frame. The rate of time dilation is then 1.5 / 2.5 = 0.6.

3b: For the nonmoving observer event B happens be at d = 1.7321 t = 3.4641. The rate of time dilation is 3 / 3.4641 = 0.8660.

3c: The time dilation increases with increased velocity.

4a: One event is 4 units of time before the other and they are separated by 5 units of space.

4b: The nonmoving observer measures d = 2.5 and t = 2.

5: At v = 0.2 c the events are simultaneous in the moving reference frame. For any velocity < 0.2 c event A happens before event B.

6: i² = -24, i² = 32.

7: a & b - timelike. c & d - spacelike. e - timelike. f - lightlike.

8a: The angle is 45^o in this example, it may otherwise be -45^o. In any and all cases it is parallel to one of the two worldlines of light passing through event A.

9a: The stay-at-home twin ages 50 y, the travelling twin ages 14 y, the difference is 36 y.

9b: 249.975 ly and back, and the total travel time is appr 7.07 y, only a little over 1/100 of the stay-at-home elapsed time!

10a: The following table shows the length contractions for several values of c when the length for the nonmoving observer is 7 units. (Rounded to 4 decimal places as in the animation.)

0.1 c d' = 6.9649
0.2 c d' = 6.8586
0.3 c d' = 6.6776
0.4 c d' = 6.4156
0.5 c d' = 6.0622
0.6 c d' = 5.6
0.7 c d' = 4.999
0.8 c d' = 4.2
0.9 c d' = 3.0512
0.95 c d' = 2.1857
0.99 c d' = 0.9875
0.999 c d' = 0.313(0)
0.9999 c d' = 0.099(0)

10b: Use this equation from the original Lorentz transformation: lorentzt . Now you want to measure along the d axis and therefore t = 0. v and d' are given and we only need to find t'. Since t = 0, the equation reduces to t' = - vd' and we easily calculate t' = -2.1. Input v, d' and t'. The animation confirms that d = 6.6776, as expected.

Sources